Struktur dan Fungsi ALU
ALU sendiri merupakan suatu kesatuan alat yang terdiri dari berbagai komponen perangkat elektronika termasuk di dalamnya sekelompok transistor, yang dikenal dengan nama logic gate, dimana logic gate ini berfungsi untuk melaksanakan perintah dasar matematika dan operasi logika. Kumpulan susunan dari logic gate inilah yang dapat melakukan perintah perhitungan matematika yang lebih komplit seperti perintah “add” untuk menambahkan bilangan, atau “devide” atau pembagian dari suatu bilangan. Selain perintah matematika yang lebih komplit, kumpulan dari logic gate ini juga mampu untuk melaksanakan perintah yang berhubungan dengan logika, seperti hasil perbandingan dua buah bilangan.
Operasi logika (logical operation) meliputi perbandingan dua buah elemen logika dengan menggunakan operator logika, yaitu :
·sama dengan (=)
·tidak sama dengan (<>)
·kurang dari (<)
·kurang atau sama dengan dari (<=)
·lebih besar dari (>)
·lebih besar atau sama dengan dari (>=)
Cara Kerja Alu
Cara Kerja CPU
Fungsi ALU
Tugas dari ALU adalah melakukan keputusan dari operasi logika sesuai dengan instruksi program. ALU melakukan operasi aritmatika yang lainnya seperti pengurangan, dan pembagian dilakukan dengan dasar penjumlahan. Sehingga sirkuit elektronik di ALU yang digunakan untuk melaksanakan operasi aritmatika ini disebut adder.
Rangkaian Utama Untuk Melakukan Perhitungan ALU
ADDER
Adder merupakan rangkain ALU (Arithmetic and Logic Unit) yang digunakan untuk menjumlahkan bilangan. Karena adder digunakan untuk memproses operasi aritmatika, maka adder juga sering disebut rangkaian kombinasional aritmatika. Ada 3 jenis Adder, yaitu:
- Rangkaian adder yang hanya menjumlahkan dua bit disebut Half Adder.
- Rangkaian adder yang hanya menjumlahkan tiga bit disebut Full Adder.
- Rangkaian adder yang menjumlahkan banyak bit disebut Paralel Adder.
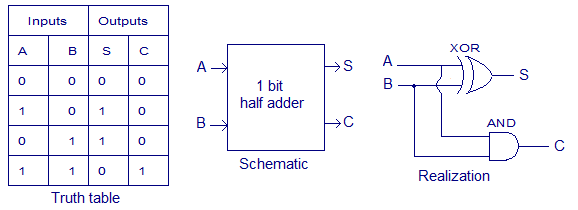
HALF ADDER
Rangkain half adder merupakan dasar bilangan biner yang masing-masing hanya terdiri dari satu bit, oleh karena itu dinamakan penjumlah tak lengkap.
1.Jika A=0 dan B=0 dijumlahkan, hasilnya S (Sum) = 0.
2.Jika A=1 dan B=0 dijumlahkan, hasilnya S (Sum) = 1.
3.Jika A=1 dan B=1 dijumlahkan, hasilnya S (Sum) = 0. Dengan nilai pindahan Cy (Carry Out) = 1
Dengan demikian, half adder memiliki dua masukan (A dan B), dan dua keluaran (S dan Cy).
Dari tabel diatas, terlihat bahwa nilai logika dari Sum sama dengan nilai logika dari gerbang XOR, sedangkan nilai logika Cy sama dengan gerbang logika AND. Dari tabel diatas, dapat dibuat rangkaian half adder.
FULL ADDER
Full adder adalah rangkaian yang bekerja melakukan perhitungan penjumlahan sepenuhnya dari dua buah bilangan binary, yang masing-masing terdiri dari satu bit. Rangkaian ini memiliki tiga input dan dua buah output, salah satu input merupakan nilai dari pindahan penjumlahan, kemudian sama seperti pada half adder salah satu outputnya dipakai sebagai tempat nilai pindahan dan yang lain sebagai hasil dari penjumlahan.
PARALEL ADDER
Paralel Adder adalah rangkaian Full Adder yang disusun secara paralel dan berfungsi untuk menjumlahkan bilangan biner berapa pun bitnya, tergantung jumlah Full Adder yang diparalelkan. Gambar dibawah ini menunjukan Paralel Adder yang terdiri dari 4 buah Full Adder yang disusun paralel sehingga membentuk sebuah penjumlahan 4 bit.
PARALEL ADDER
Paralel Adder adalah rangkaian Full Adder yang disusun secara paralel dan berfungsi untuk menjumlahkan bilangan biner berapa pun bitnya, tergantung jumlah Full Adder yang diparalelkan. Gambar dibawah ini menunjukan Paralel Adder yang terdiri dari 4 buah Full Adder yang disusun paralel sehingga membentuk sebuah penjumlahan 4 bit.
---------------------------------------
---REPRESENTASI INTEGER---
----Bagian Presentasi Muhammad Sobirin - 14117254 - 2KA32----
Negasi
Untuk membuat negasi gunakan komplement dua.
Untuk bilangan positif, komplemen dua adalah sama dengan sistem yang menunjukkan tanda dan besarnya bilangan, yaitu MSB yang digunakan sebagai penunjuk atau tanda bilangan, dan bit-bit sisanya menunjukkan besarnya.
Untuk bilangan negatif, komplemen dua dapat diperoleh dengan menghitung terlebih dahulu komplemen satu dari bilangan biner semula (yang bertanda positif), kemudian menambahkan 1 ke LSB-nya.
Contoh :
+7(10) = 0111(2)
-7 (10) = 1001(2)
Cara Untuk mencari komplement ke dua dari 7(2). Cari dulu komplement satu nya, yaitu :
7(10) = 0111(2)
komplement satu : 1000(2)
1
--------- +
Komplement dua : 1001(2)
Jadi, -7(10) = 1001(2)
Aturan Untuk Mendeteksi Overflow
Aturan overflow
Bila dua buah bilangan di tambahkan, dan keduanya positif atau keduanya negatif maka over flow akan terjadi jika dan hanya jika hasilnya memiliki tanda yang berlawanan.
Contoh :
0011 = 3
0100 = 4
------------- +
0111 = 7 (bukan overflow)
0101 = 5
0100 = 4
------------- +
1001 = 9 (overflow)
Pembulatan
Teknik pembulatan yang sesuai dengan standard IEEE adalah sebagai berikut :
Pembulatan ke Bilangan Terdekat : Hasil dibulatkan ke bilangan terdekat yang dapat direpresentasi.
Pembulatan Ke Arah : Hasil dibulatkan ke atas ke arah tak terhingga positif.
Pembulatan Ke Arah : Hasil dibulatkan ke atas ke arah tak terhingga negatif.
Pembulatan Ke Arah 0 : Hasil dibulatkan ke arah 0
Konversi Bilangan
Bilangan
Bilangan biner (Bilangan berbasis dua, bilangannya: 0,1)
Bilangan octal (Bilangan berbasis delapan bilangannya: 0,1,2,3,4,5,6,7)
Bilangan desimal (Bilangan berbasis sepuluh, bilangannya: 0,1,2,3,4,5,6,7,8,9)
Bilangan hexadesimal (Bilangan berbasis enam belas, bilangannya: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)
Konversi bilangan biner, octal atau hexadesimal menjadi bilangan desimal.
Konversi bilangan desimal menjadi bilangan biner, octal atau hexadesimal.
Konversi bilangan octal ke biner dan sebaliknya.
Konversi bilangan hexadesimal ke biner dan sebaliknya.
Konversi bilangan hexadesimal ke octal dan sebaliknya
Floating-Point Representaion
Representasi Integer oleh Biner
Dalam sistem bilangan biner ada 4 macam sistem untuk merepresentasikan integer
- representasi unsigned integer
- representasi nilai tanda (sign magnitude)
- representasi bias
- representasi komplemen dua (2’s complement)
Unsigned Integer
Untuk keperluan penyimpanan dan pengolahan komputer diperlukan bilangan biner yang terdiri atas 0 dan 1
1 byte (8 bit binary digit) dapat digunakan untuk menyatakan bilangan desimal dari 0 – 255
Kelemahan Unsigned Integer
·Hanya dapat menyatakan bilangan positif
·Sistem ini tidak bisa digunakan untuk menyatakan bilangan
integer negatif
Representasi Nilai Tanda (sign magnitude)
Karena kelemahan unsigned integer, Dikembangkan beberapa konvensi untuk menyatakan bilangan integer negatif
Konvensi
Perlakuan bit yang paling kiri (MSB) di dalam byte sebagai tanda
Bila MSB = 0 maka bilangan tersebut positif
Jika MSB = 1 maka bilangan tersebut negatif
Kelemahan sign magnitude
Adanya representasi ganda pada bilangan 0, yaitu
Representasi Nilai Tanda (sign magnitude)
Karena kelemahan unsigned integer, Dikembangkan beberapa konvensi untuk menyatakan bilangan integer negatif
Konvensi
Perlakuan bit yang paling kiri (MSB) di dalam byte sebagai tanda
Bila MSB = 0 maka bilangan tersebut positif
Jika MSB = 1 maka bilangan tersebut negatif
Kelemahan sign magnitude
Adanya representasi ganda pada bilangan 0, yaitu
Representasi BIAS
Digunakan untuk menyatakan exponen (bilangan pemangkat) pada representasi floating point.
Dapat menyatakan bilangan bertanda, yaitu dengan mengurutkan dari bilangan negatif terkecil dapat dijangkau sampai bilangan positif paling besar yang bisa dijangkau.
Mengatasi permasalahan pada sign magnitude yaitu +0 dan -0.
Representasi Komplemen 2
Merupakan perbaikan dari representasi nilai bertanda (sign magnitude) yang mempunyai kekurangan pada operasi penjumlahan dan pengurangan serta representasi nilai 0.
Bilangan Negatif Pada 2’s Complement
1. Sistem bilangan dalam 2’s complement menggunakan bit paling kiri (MSB) sebagai bit tanda dan sisanya sebagai bit nilai seperti pada sign magnitude
2. Bilangan negatif dalam 2’s complement dibentuk dari:
· komplemen satu dari bilangan biner semula (nilai positif)
· menambahkan 1 pada LSB
Floating-Point Aritmatika
Aritmatika floating point penjumlahan/pengurangan
Perkalian
Pembagi
Aritmatika floating point penjumlahan/pengurangan
Langkah langkah yang dilakukan untuk menambah/mengurangkan dua bilangan floating point :
Bandingkan kedua bilangan, dan ubah ke bentuk yang sesuai pada bilangan dengan nilai exponensial lebih kecil
Lakukan operasi penjumlahan / pengurangan
Lakukan normalisasi dengan ’menggeser’ nilai mantissa dan mengatur nilai exponensialnya
contoh :
123 x 102 123 x 102
456 x 10-2 + 0,0456 x 102
123,0456 x 102
Perkalian
Algoritma umum untuk perkalian dari bilangan floating point terdiri dari tiga langkah:
Hitung hasil exponensial dengan menjumlahkan nilai exponent dari kedua bilangan
Kalikan kedua bilangan mantissa
Normalisasi hasil akhir
contoh :
123 x 102 123 x 102
456 x 10-2 x 0,0456 x 102
Exp : 2 x 2 = 4
Mantissa : 123 x 0,0456 = 5,6088
Normalisasi : 5,6088 x 104
Pembagian
logoritma umum untuk pembagian dari bilangan floating point terdiri dari tiga langkah :
Hitung hasil exponensial dengan mengurangkan nilai exponent dari kedua bilangan
Bagi kedua bilangan mantissa
Normalisasi hasil akhir
contoh :
123 x 102 123 x 102
456 x 102 ÷ 456 x 102
Exp : 2 - 2 = 0
Mantissa : 123 ÷ 456 = 0,2697
Normalisasi : 2,697 x 10-1
Sumber :
https://prezi.com/si9g2qoihbdo/aritmatika-komputer/
http://isdesember.blogspot.com/2014/11/aritmatika-komputer.html?m=1
https://riskydwiyanti.wordpress.com/2013/10/20/integer-representation/
http://firmaninformatika.blogspot.com/2014/12/integer-arithmetic.html
http://blograkata.blogspot.com/2012/02/pengertian-adder.html
http://tuankaru.blogspot.com/2016/11/definisifungsi-dan-cara-kerja-alu.html
http://sangbadrun.blogspot.com/2015/07/pengertian-fungsi-dan-cara-kerja-cpu.html
http://hyperpost.blogspot.com/2014/04/konversi-bilangan-biner-octal-desimal.html
https://studylibid.com/doc/414497/representasi-floating-point